
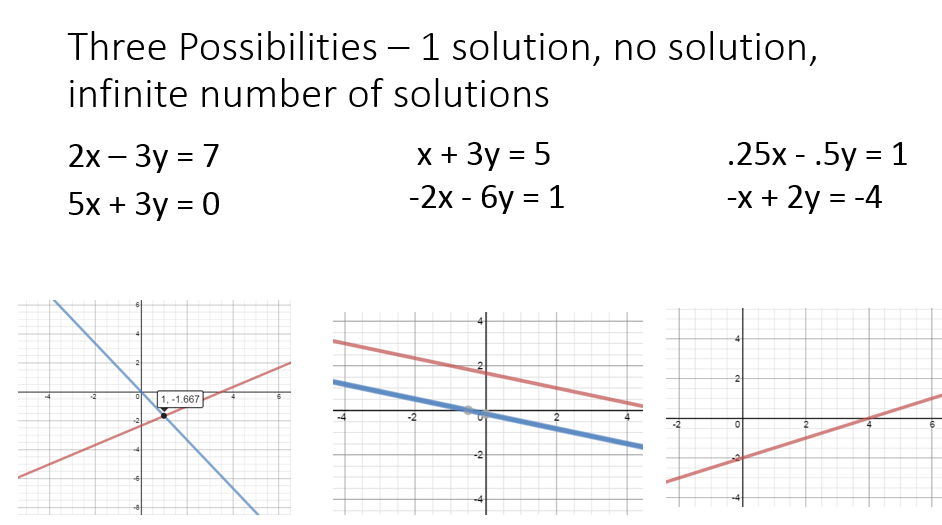
Three possible outcomes for solutions to systems of equations What happens if the lines never cross, as in the case of parallel lines? How would you describe the solutions to that kind of system? In this section, we will explore the three possible outcomes for solutions to a system of linear equations. As we saw in the last section, if you have a system of linear equations that intersect at one point, this point is a solution to the system. There are an infinite number of solutions. Recall that a linear equation graphs as a line, which indicates that all of the points on the line are solutions to that linear equation. Use a graph to classify solutions to systems In the next section, we will work with systems that have no solutions or infinitely many solutions. In this section we have seen that solutions to systems of linear equations and inequalities can be ordered pairs. Consider the graph of the inequality y<2x+5.

On the other side, there are no solutions. Remember from the module on graphing that the graph of a single linear inequality splits the coordinate plane into two regions. On one side lie all the solutions to the inequality. When you graph a system of linear inequalities on the same set of axes, there are a few more things you will need to consider. Graphing a system of linear equations consists of choosing which graphing method you want to use and drawing the graphs of both equations on the same set of axes. In the next section, we will see that systems with two of the same equations in them have an infinite number of solutions. When you graph them, they are the same line. If you were to write them both in slope-intercept form you would see that they are the same equation. \beginx+2and 2y-x=4 are really the same equation, expressed in different ways. Substitute y = 0 in to the equation to find the x-intercept. We can use tables of values, slope and y-intercept, or x– and y-intercepts to graph both lines on the same set of axes.įor example, consider the following system of linear equations in two variables. The same techniques are used to graph a system of linear equations as you have used to graph single linear equations. First, we will practice graphing two equations on the same set of axes, and then we will explore the different considerations you need to make when graphing two linear inequalities on the same set of axes.

In this section, we will look at systems of linear equations and inequalities in two variables. In this section, we will explore some basic principles for graphing and describing the intersection of two lines that make up a system of equations. Accidents, time of day, and major sporting events are just a few of the other variables that can affect the flow of traffic in a city. It is rare to find, for example, a pattern of traffic flow that that is only affected by weather.

They are a useful tool for discovering and describing how behaviors or processes are interrelated. You will find systems of equations in every application of mathematics. A system of linear equations can help with that.Ī system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously.
If you want to best describe its flow, you must take into account these other variables. The way a river flows depends on many variables including how big the river is, how much water it contains, what sorts of things are floating in the river, whether or not it is raining, and so forth.


 0 kommentar(er)
0 kommentar(er)
